Reelle datasett: Derivasjon (R/FYS)

Reelle datasett: Derivasjon (R/FYS)#

Endring er veldig viktig i naturvitenskap.

Numerisk derivasjon på et datasett#

La oss ta et fysisk eksempel med ekte data om en terning som faller. Datasettet finner du her. Datasettet er samlet inn ved hjelp av video og Tracker.

import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv("fallende_terning.csv", decimal=".", delimiter=";")

t = df["t"]
y = df["y"]

plt.xlabel("tid (sekunder)")
plt.ylabel("y (meter)")
plt.scatter(t, y)
plt.show()
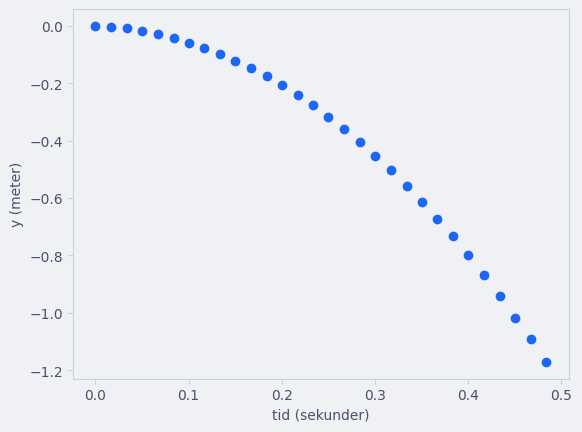
../_images/07b538a985be893c99adca7968bc4d650d0d15009d60a9f9da1197787510abdc.png

Hvis vi deriverer posisjonen så får vi farten til en gjenstand. Den deriverte kan vi finne numerisk ved å bruke gjennomsnittlig vekstfart \(v_n=\frac{\Delta y}{\Delta t}=\frac{y_{n + 1} - y_{n}}{t_{n + 1} - t_{n}}\).

Tidssteg

Innsamling av fysiske data er blant annet begrenset av hvor fine tidssteg vi har. Når jeg samlet inn data til dette eksperimentet filmet jeg med et kamera på \(60\) FPS. Det betyr at det blir tatt \(60\) bilder per sekund, noe som gjør at avstanden mellom hver tid blir \(\frac{1}{60}\approx 0.0167\) sekunder.

Avstanden mellom hver måling i tid blir det samme som \(dx\) i derivasjonen. Desto høyere FPS, desto bedre blir resultatet.

import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv("fallende_terning.csv", decimal=".", delimiter=";")

t = df["t"]
y = df["y"]

v = []
for n in range(len(t) - 1): # Vi må stoppe før den siste verdien
    dy = y[n + 1] - y[n] # Endring i y-posisjon
    dt = t[n + 1] - t[n] # Endring i tid
    v.append(dy / dt)

# Ved å bruke fremoverdifferanse mangler vi den siste verdien.
# Da kan vi bruke bakoverdifferanse.
dy = y.iloc[-1] - y.iloc[-2]
dt = t.iloc[-1] - t.iloc[-2]
v.append(dy / dt)

plt.xlabel("tid (sekunder)")
plt.ylabel("fart (meter per sekund)")
plt.scatter(t, v)
plt.show()
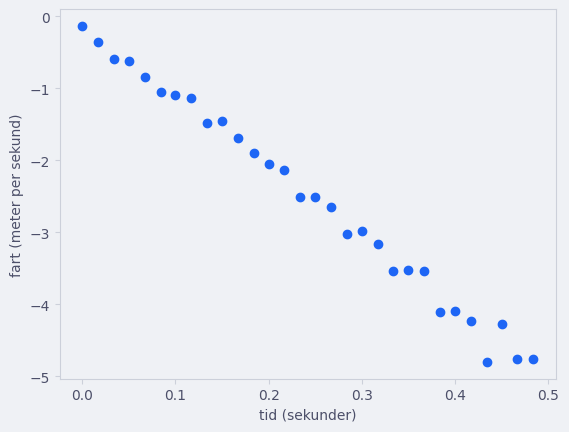
../_images/14c5c4b76092403f47c3181e6197378e906b8b4e2d5da6a737d2d5a7c74ccc07.png

Nå har vi derivert numerisk! Legg merke til at farten ser ut til å være ganske lineær.

Før vi ser videre på den fysiske tolkningen, la oss se på en litt enklere metode for å finne numerisk derivert ved å bruke np.gradient().

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

df = pd.read_csv("fallende_terning.csv", decimal=".", delimiter=";")

t = df["t"]
y = df["y"]

v = np.gradient(y, t) # Derivert av y med hensyn på t

plt.xlabel("tid (sekunder)")
plt.ylabel("fart (meter per sekund)")
plt.scatter(t, v)
plt.show()
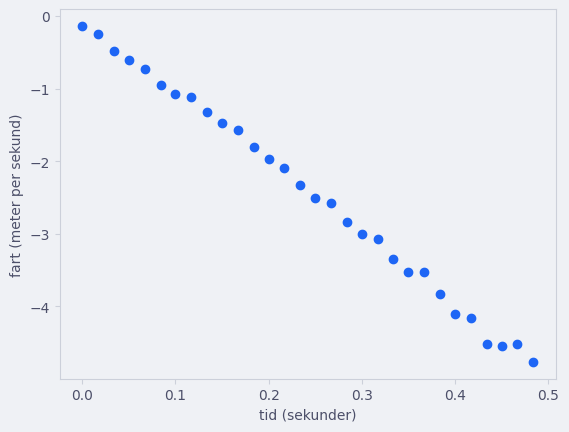
../_images/08d8be2e2bdb756b6f8dc9d6490a62df3a5a66f9833cd5ef98cca4c5e19f5168.png

Det var mye enklere. Legg også merke til at vi får litt andre verdier. Disse verdiene er faktisk bedre approksimasjoner for den deriverte, fordi np.gradient() bruker sentraldifferanse på alle punktene i midten.

En fysisk tolkning#

Farten vi regnet ut så ganske lineær ut. Det er ikke så rart. En ting som faller fritt (uten luftmotsand) fra \(y=0\) vil følge kurven \(y(t)=-\frac{1}{2}gt^2\) der \(g\) er en konstant som kalles for tyngdeakselerasjonen. Farten vil da bli gitt ved \(v(t)=y'(t)=-gt\) som er en lineær funksjon. Dette har vi vist at stemmer ved å derivere numerisk!

La oss bruke regresjon for å finne en verdi for tyngdeakselerasjonen \(g\). Hvis man slår opp tyngdeakselerasjonen på jorden får man \(g\approx 9.81\). La oss se hvor godt vårt eksperiment passer.

import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

df = pd.read_csv("fallende_terning.csv", decimal=".", delimiter=";")

t = df["t"]
y = df["y"]

def modell_y(t, g):
    return - 0.5 * g * t **2

g = curve_fit(modell_y, t, y)[0][0]

print(f"Modellen vår finner en verdi for g = {g:.4f} m/s^2")

plt.scatter(t, y, label="Posisjon")
plt.plot(t, modell_y(t, g), label=f"Modell for g = {g:.2f}", color="red")
plt.plot(t, modell_y(t, 9.81), label=f"Modell for g = 9.81", color="orange")
plt.xlabel("tid (sekunder)")
plt.ylabel("y (meter)")
plt.legend()
plt.show()

Modellen vår finner en verdi for g = 10.0142 m/s^2
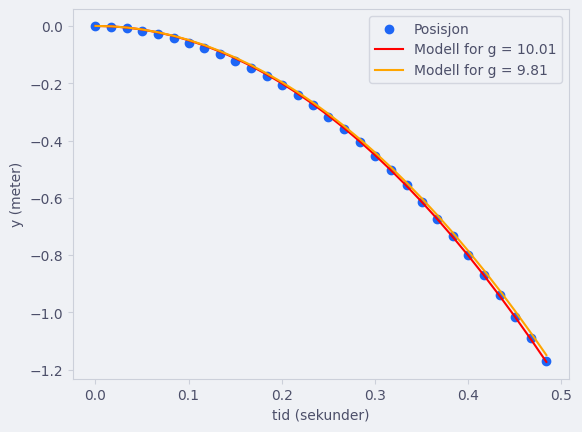
../_images/bec7f66dfeb0bc70fd05d556f45a911407079f55a101ec0e1ed51d1fab0ea2a5.png

Utforsk din egen problemstilling.

Finn data om et naturvitenskapelig fenomen eller lag dine egne data f.eks ved å sette opp et eksperiment, filme og bruke Tracker. Et annet alternativ er phyphox, en app som lar deg samle inn masse forskjellige data med sensorene på mobilen.

Gjennomfør derivasjon og/eller regresjon for å si noe om fenomenet. Det kan for eksempel være

  • Å finne en verdi for tyngdeakselerasjonen \(g\) ved å sette opp et fysisk forsøk

  • Sammenlikne ulike ting som faller for å verifisere at de faller med samme akselerasjon

  • Undersøke smittespreding ved å se på COVID-tall.

  • Undersøke data over globale temperaturer

… eller hva som helst annet som interesserer deg.

Contents