Matematiske funksjoner

I denne delen skal vi lære om plotting.

For å plotte skal vi bruke en pakke som heter matplotlib. Mange Python-installasjoner vil inkludere denne pakken, men man kan også installere pakken ved å skrive pip install matplotlib i terminalvinduet.

Et enkelt plot

La oss plotte den matematiske funksjonen \(x^2\) i intervallet \([0, 5]\).

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return x**2 # Definerer funksjonen

x = np.linspace(0, 5, 100) # Hundre punkter mellom 0 og 5
y = f(x) # Setter x inn i funksjonen f. y blir da funksjonsverdier

plt.plot(x, y) # Lager plot
plt.show() # Viser plot

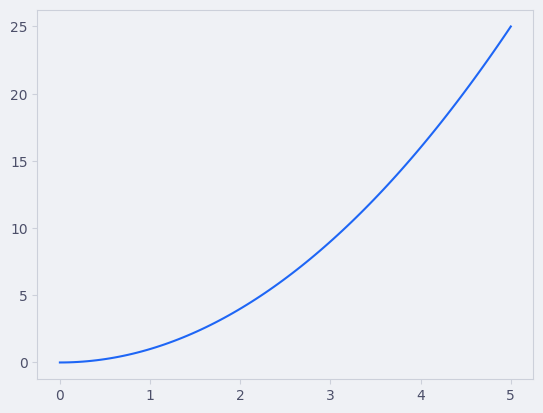
Stil

«Du må ha med navn på aksene! 😠» - En gretten mattelærer (sikkert)

La oss få med litt stil på plottene våre.

import numpy as np
import matplotlib.pyplot as plt

def f(x):
    return x**2

def g(x):
    return x**3

x = np.linspace(0, 5, 100)

plt.title("Sammenlikning av x**2 og x**3") # Tittel
plt.xlabel("x-verdier") # Gir navn til x-aksen
plt.ylabel("funksjonsverdier") # Gir navn til y-aksen
plt.plot(x, f(x), label="f(x)=x**2") # label gir navn til funksjonen
plt.plot(x, g(x), label="g(x)=x**3", color="red") # label gir navn til funksjonen, color gir farge
plt.grid() # Viser rutenett
plt.legend() # Lager boksen med funksjonenes navn
plt.show() # Viser plottet

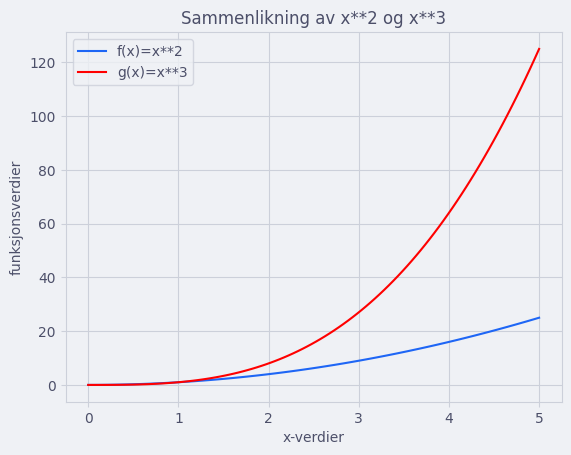
«Wow! For et fint plott! 🤓» - En fornøyd mattelærer (sikkert)

Undersøk koden grundig. Legg merke til hvordan vi kan sette inn funksjonsverdier i selve plot()-funksjonen.

Legg også merke til hvordan vi kan plotte flere grafer med plot() før vi kjører show()-funksjonen. Vi kan tenke på plot() som en funksjon som tegner og show() som å en funksjon som viser det vi har tegnet.

Endre på aksene

Aksene for plottet settes automatisk, men hvis vi ønsker å endre på disse så kan vi bruke plt.xlim()- og plt.ylim()-funksjonene.

• plt.xlim(start, slutt) gjør at plottet bare viser x-verdier mellom start og slutt.

• plt.ylim(start, slutt) gjør at plottet bare viser y-verdier mellom start og slutt.

---

Oppgaver

Oppgave 1

Overskuddet \(O(x)\) til en bedrift etter å ha produsert \(x\) enheter er gitt ved \(O(x)=-x^2+50x-96\).

1. Plott den matematiske funksjonen O(x) med \(100\) jevnt fordelte punkter mellom \(0\) og \(50\). Få med tittel og navn på aksene.

2. Hvor mange enheter må bedriften lage for å tjene penger? Les av i plottet.

3. Hvor mange enheter må bedriften lage for å tjene mest mulig penger? Les av i plottet.

Oppgave 2

Lag en array x med 100 jevnt fordelte tall i intervallet \([-2, 2]\).

Plott disse matematiske funksjonene i samme koordinatsystem:

1. \(f(x) = x+2\)

2. \(g(x) = x^2\)

3. \(h(x) = abs(x)\)

Få med label på hver funksjon, og bruk plt.legend for å vise hvilken funksjon som er hvilken.

• I hvilke punkter krysser de forskjellige funksjonene hverandre? Hvilke funksjoner er det som krysses?

Skriv svaret som en kommentar.